Колебания — это процессы, которые имеют какую либо степень повторяемости во времени.
Свободные (собственные) колебания — это колебания, которые предоставляют сами себе системы, вызванные первоначальным кратковременным внешним возбуждением.
Колебательная система — это такая система, которая способная производить свободные колебания.
Колебательная система соответствует следующим условиям:
- необходимо положение устойчивого равновесия;
- необходим фактор, не позволяющий системе остановиться в положении равновесия в процессе колебаний;
- трение в системе должно быть небольшим, а собственная частота колебательной системы обусловливается только параметрами системы.
Амплитуда колебаний — это максимальное значение величины (для механических колебаний это смещение), которая совершает колебания.
Период колебаний — это самый маленький отрезок времени, через который система совершает колебания, снова возвращается в исходное состояние, т. е. в начальный момент.
Частота колебаний — это физическая величина, равная числу колебаний, которые совершаются в единицу времени.
Циклическая частота — это характеристика гармонических колебаний, совершаемых за
Фаза колебаний — это аргумент функции, который периодически изменяется.
Затухающие колебания — это собственные колебания, у которых амплитуда уменьшается со временем, что обусловлено потерями энергии колебательной системой.
Коэффициент затухания и логарифмический декремент затухания — это характеристика быстроты уменьшения амплитуды в случае механических колебаний, где энергия убывает за счет действия сил трения и других сил сопротивления.
Декремент затухания — это количественная характеристика быстроты затухания колебаний, которая определяется натуральным логарифмом отношения двух последовательных максимальных отклонений 
, колеблющейся величины в одну сторону: 
Декремент затухания — величина, обратная числу колебаний, по истечении которых амплитуда убывает в: е раз е = 2,71828). Промежуток времени, необходимый для этого, называется временем релаксации.
Дифференциальное уравнение малых затухающих колебаний системы:
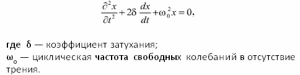
Вынужденные колебания — это колебания, которые возникают под действием внешней периодической силы.
Дифференциальное уравнение вынужденных колебаний:
Резонанс — это процесс резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты 
, вынуждающей силы к собственной циклической частоте 
колебательной системы.
Автоколебания — это незатухающие колебания физической системы, которые способны существовать без воздействия на нее внешних сил.
Автоколебательная система — это физическая система, где имеет место существовать автоколебания.
Автоколебательная система состоит из следующих частей:
- колебательная система, в которой параметры определяют частоту автоколебаний;
- источник энергии, который способствует поддержанию колебаний;
- клапан, который регулирует поступление энергии в колебательную систему;
- положительная обратная связь, которая способна управлять клапаном в колебательной системе.
Обратная связь — это воздействие результатом какого-либо процесса на его протекание.
Обратная связь бывает:
положительная — это связь, которая приводит к увеличению отклонения;
отрицательная — это связь, которая приводит к уменьшению отклонения;
Периодические колебания — это колебания, которые имеют изменяющиеся значения физических величин, но которые повторяются через равные отрезки времени.
Смещение — это физическая величина, которая является характеристикой колебаний, равная отклонению тела от положения равновесия в данный момент времени.
Математический, физический, пружинный маятники
Математический маятник — это тело малых размеров, подвешенное на тонкой нерастяжимой нити, масса которой ничтожно мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 
уравновешивается силой натяжения нити 
.
Составляющая силы тяжести при отклонении маятника из положения равновесия на некоторый угол ф 
, где знак «минус» означает, что касательная составляющая на- правлена в сторону, противоположную отклонению маятника. Второй закон Ньютона для математического маятника запишется: 
, где x — линейное смещение маятника от положения равно- весия по дуге окружности, l — радиус.
Угловое смещение будет равно 
Для малых колебаний математического маятника второй закон
Ньютона записывается в виде:
Если математический маятник совершает малые колебания, то он является гармоническим осциллятором. Собственная частота малых колебаний математического маятника:
Период малых колебаний математического маятника определяется:
Физический маятник — это тело, которое является твердым, производящее колебания в поле каких-либо сил относительно точки, которая не является центром масс этого тела, или горизонтальной оси.
Второй закон Ньютона для физического маятника принимает вид:
Собственная частота малых колебаний физического маятника:
Период малых колебаний физического маятника определяется:
Круговая частота свободных колебаний физического маятника определяется выражением:
Центр качания физического маятника — это точка, где необходимо сосредоточить всю массу физического маятника, чтобы его период колебаний оставался постоянным.
Физический маятник обладает следующим замечательным свойством: если физический маятник подвесить за центр качания, то его период колебаний будет постоянным, а прежняя точка подвеса станет новым центром качания.
Пружинный маятник — это колебательная система, которая состоит из груза, подвешенного к абсолютно упругой пружине.
Пружинный маятник совершает гармонические колебания с циклической частотой:
, где k — коэффициент жесткости.
Период пружинного маятника определяется:
Уравнение движения пружинного маятника при этом имеет вид:
