Любая концепция способна породить свою управленчески значимую “цифровую” статистику /…/ Но ни одна цифровая статистика, в том числе деньги и “ценные” бумаги, не способна породить концепцию жизнестроя общества, гармонично развивающегося в биосфере планеты.
“Основы теории подобия макроэкономических систем” Авторский коллектив ВП СССР
Современная система мѣръ. В основе современной системы мѣръ лежит совокупность взаимосвязанных между собой эталонов. Данные эталоны были выбраны исторически и юридически закреплены на международном уровне в ходе XI Генеральной конференцией по мѣрам и весам (ГКМВ) в 1960 г. (закрепленная система получила название Система СИ и к настоящему времени в качестве основной изпользуется большинством стран мира). Впервые важнейшие эталоны системы СИ стали широко применятся после Французской революции в конце ХIX века. Базовыми принципами выбора эталона в любой эталонной системе мѣръ являются: 1) принцип удобства изпользования, 2) принцип неизменности эталона (в качестве эталона не может изпользоваться объект параметры которого изменяются или варьируются во времени) и 3) принцип возможности восстановления эталона в случае его утраты.
Таким образом, априори, любой эталон должен быть восстанавливаемым с высокой долей точности путем осуществления определенной последовательности шагов.
Основными единицами измерения современной системы мер являются: метр (пространственная мѣра), килограмм (мѣра веса), литр (мѣра объема), секунда (мѣра времени), кельвин (температура).
- Метр – изначально это длина маятника с частотой колебаний равной 1 секунде[1].
- Литр – 1 кубический дециметр чистой воды.
- Килограмм – масса 1 литра воды при температуре 0 С.
- Кельвин – ноль К (- 273,15 С) – условная температура при которой колебания частиц в узлах любой кристаллической решетки равны нулю, а шаг шкалы равен 1 С. Градусы Цельсия, 0 С – температура замерзания чистой воды, 100 С – температура кипения чистой воды при давлении 760 мм.рт.ст. Шаг шкалы определяется делением на 100 частей температурной разности между точкой кипения и замерзания чистой воды.
Таким образом, видно, что в основе большинства основных современных единиц измѣрения лежит секунда. Что же такое секунда?
Считается, что секунда получена делением минуты на 60 равных долей. Минута получена делением часа на 60 равных долей. Час получен делением суток на 24 равные доли. Сутки же равняются периоду времени за который земной шар совершает полный оборот вокруг своей оси. Возникает вопрос: Почему деление величин осуществлялось на 24 и 60 долей?
Наличие этих чисел ясно указывает на пропорцию лунного цикла, изпользуемую для измерения времени. В году умещается 12 целых долей лунного цикла, а в синодическом месяце 30 солнечных суток (29,53058812). Отсюда изпользование данных пропорций для измерения всех вложенных явлений, связанных со временем. День – подобен году – следовательно он должен состоять из 12 частей, а час – подобен месяцу (который имеет 30 дней и 30 ночей), следовательно он состоит из 60 долей[2].
Безэталонные системы мѣръ. В основе большинства систем мѣръ до Нового времени лежали размеры человеческого тела. Данные системы существовали многие вѣка и в полной мѣре соответствовали крылатому выражению “человек – мѣра всех вещей”. Установлено, что многие произведения архитектурного искусства (в том числе знаменитые египетские пирамиды) созданы с изпользованием именно такой системы мѣръ. В качестве примѣра возьмем древнерусскую систему мѣрных сажений (остатки безэталонной системы мѣръ сохранились также в Англии и США, хотя в нынешнем виде ее уже нельзя назвать таковой). Чтобы разобраться в принципах функционирования подобных систем необходимо ответить на ряд закономерных вопросов:
1) Каким образом индивидуальные длины частей тела множества людей были усреднены до стандартной длины?
2) Каким образом эта длина сохранялась в течение столетий и тысячелетий при отсутствии каких бы то ни было общегосударственных стандартных эталонов?
3) Какие обстоятельства способствовали превращению разрозненных несоизмеримых инструментов в единую взаимосвязанную систему и в чем это единство заключается?
Начнем с третьего вопроса. Установлено, что в древнерусской системе мѣръ имелся целый ряд величин с идентичным названием (саженей, то есть условное расстояние между концами пальцев разведенных в стороны рук), имеющих однако различную длину: сажень городовая 284,8 см, сажень без названия 258,4 см, сажень великая 244,0 см, греческая 230,4 см, казенная 217,6 см, царская 197,4 см, церковная 186, 4 см, народная 176,0 см, кладочная 159,7 см, простая 150,8 см, малая 142,4 см, без названия 134,5 см и т.д.
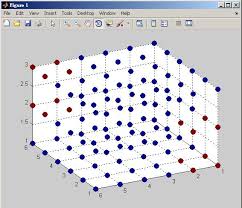
Совокупность этих мѣръ выстраивается в матрицу, в основе которой лежат их пропорциональные отношения (см. рисунок). В качестве базисной единицы может быть взята практически любая величина (сажень любого человека). Каждое из направлений (диагоналей расходящихся от единицы) креста содержит свой коэффициент пропорциональности — знаменатель: главная диагональ — Ф = 1,615 (золотая пропорция) основной базисный ряд — 2,0 (бинарная пропорция), перпендикулярная диагональ — 2,472… и базисная строка — 1,236…[3] Следовательно связующим элементом безэталонных систем мѣръ выступали не абсолютные величины, а величины пропорций и характер их взаимосвязей, описываемых специальными матрицами.
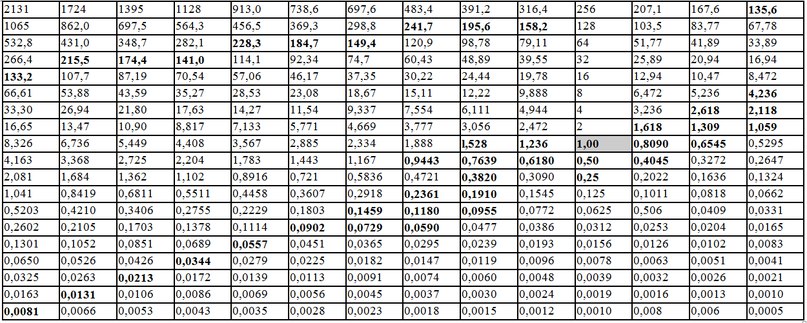
Каким же образом выявленные нами пропорции, которые лежали в основе объединяющей матрицы (всемѣра) сохранялись в течение столетий и тысячелетий при отсутствии каких бы то ни было общегосударственных стандартных эталонов, и как они могли быть легко восстановлены? Для этих целей изпользоваля “метод вавилонов”, “метод наугольников” и пр. (приведены современные названия).
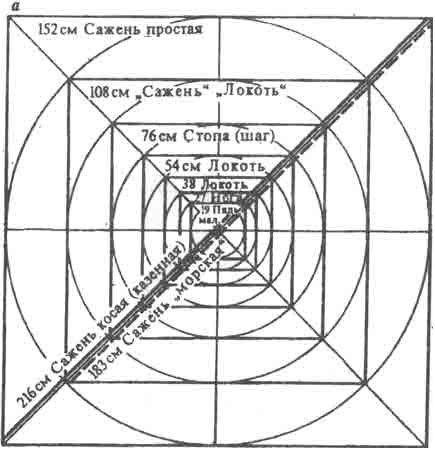В случае, когда в наличии имелся образец сажени, для восстановления утраченных величин пропорций изпользовался “метод вавилонов”, который заключался в построении квадрата с длиной стороны равной сажени с дальнейшим выстраиванием череды меньших квадратов, на основе вписанных в квадрат окружностей и его диагоналей.
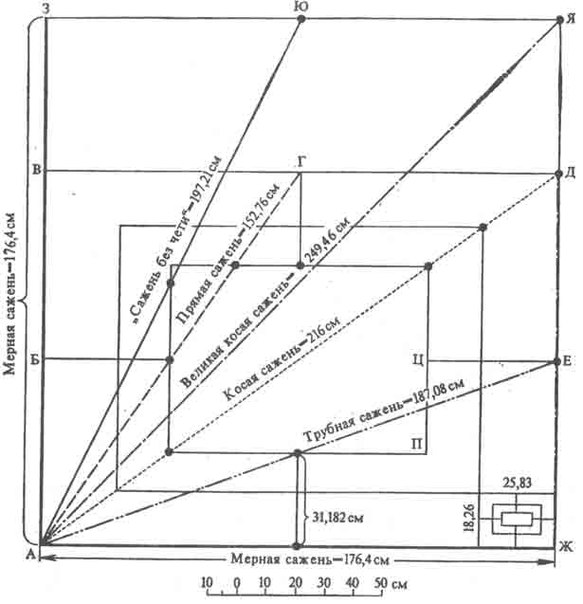В случае же если образца сажени не было в наличии для восстановления системы пропорций брался деревянный пруток произвольной длины. Возьмем для примѣра рост плотника 172 см, что почти соответствует мѣрной (маховой) сажени, и примем его за базисную длину. Если три прутка данной длины сложить равнобедренным наугольником, то высота в нем будет равна 148,96 см, что по структуре соответствует сажени простой, да и по длине близко к ней. Если к центру мѣрной сажени под прямым углом приставить другую мѣрную сажень и соединить их свободные концы длинными прутками, то получим равносторонний наугольник, длинные стороны которого равны 192,30 см, а это аналог “сажени без чети” и т.д[4]. Искомые пропорции найдены. Таким образом, вся система легко восстанавливалась на основе пропорций правильных геометрических фигур или человеческого тела.
Интересен метод воспроизводства архитектурных деталей и сооружений кругового очертания. Для этого изпользовали сажень разделенную на 21 равную часть (примеры такого деления обнаружены на найденном при раскопках в Новгороде “новгородском мериле”). Причины такого деления заключаются в существовании следующей пропорции: когда диаметр делится на 21 часть, в самом круге с большой точностью будут укладываться 66 таких же частей. Это деление известно с древности как отношение Архимеда в виде пропорции 66:21 = 22:7 = 3,1428, что и обусловливает возможность построения любой окружности с точностью до 0,05% и проведения операции перевода окружности и отрезка любой окружности (дуги) в линейные мѣры[5].
И наконец последний вопрос, связанный с безэталонными системами мѣръ[6] заключался в нахождении усредненной величины мѣры, необходимой при массовом изпользовании напримѣр при ведении торговли и обмена на ярмарках. К сожалению данный вопрос не имеет однозначного решения, однако с высокой долей вероятности можно предположить, что решался он на основе закона больших чисел, который гласит, что средняя арифметическая величина достаточно большой конечной выборки близка к теоретическому среднему (математическому ожиданию) этого распределения (см. рисунок). И чем больше выборка, тем меньше расхождение между ожидаемой математической средней и реальной средней величиной искомого. В качестве условной задачи, демонстрирующей практическую реализацию “закона”, можно привести задачу нахождения меры длины для изпользования ее в ходе торговли на ярмарке: каждый входящей предоставляет для измерения свой локоть, а результирующая средняя величина становится изходным мерилом принимаемым в качестве эталона для данного события общественной жизни. При этом массовость события будет выступать в качестве гаранта отсутствия значительного отклонения величины от “нормальной”.[7] (мы также полагаем, что данный способ восстановления сажени не противоречит выдвинутым другими изследователями утверждением о том, что древнерусские мѣрила были строго пропорциональны размерам нашей планеты, поскольку человеческий организм и “земля-матушка” – части одного природного процесса)[8].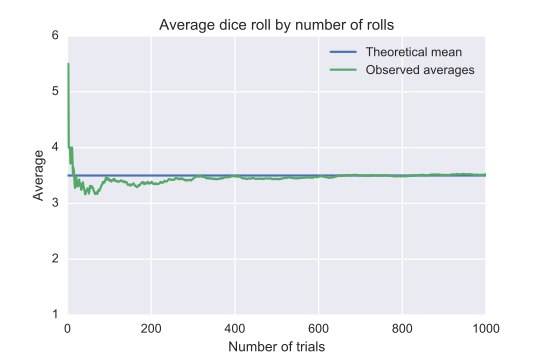
Результатом такого подхода являлось нарастание системной точности, с каждым новым измѣрением, в то время как в современной системе мѣръ заложено нарастание системной ошибки, поскольку с каждым новым измѣрением растет вероятность все большего отклонения получаемой величины от эталона.
Также хотелось бы в рамках данной статьи немного подробнее коснуться темы матриц.[9] Матрицы – представляют собой многомѣрную совокупность (поле) взаимосвязанных математических прогрессий (последовательностей).[10] Самый простой пример – двухмѣрная матрица (такую матрицу можно легко построить в Exel) являющаяся совокупностью строк и столбцов, на пересечении которых находятся её элементы, расположенные относительно друг друга согласно определенной пропорции (находящиеся в определенной зависимости друг от друга)[11].
Простейшими примѣрами двухмерных матриц могут служить: Нулевая матрица, Единичная матрица, Диагональная матрица, Транспонированная матрица, Матрица единиц, Матрица сдвига, Матрица перестановки, Бинарная (двоичная) матрица и т.д.
Для наделения совокупности точек пространства, описываемых матрицей, бОльшим количеством характеристик (мѣрностей) изпользуются системы многомѣрных взаимовложенных матриц.
Возникает вопрос, каким образом можно (“матрично”) согласовать более двух явлений и всегда ли это возможно? Для гармоничного (без разрушения одной из систем в длительной перспективе) соединения трех и более систем изпользуется такое математическое понятие как “вурф”. Термином “вурф” (в немецком языке – бросок, скачок) в математике обозначается сложное соотношение частей трехчастных объектов, а золотой вурф отражает гармоничное взаимное состояние частей и в целом динамики всего объекта. Доказано, что если значения двух или более вурфов систем равны друг другу, то эти системы относятся к одному и тому же природному процессу. И, следовательно, эти системы могут быть совмещены или взаимно вложены без нарушения их структур (могут существовать совместно очень долго). Значение вурфа определяется по формуле: W(a, b, c) = (a+b)*(b+c)/b*(a+b+c).
Кроме того, известно, что “почленные части трехчастного деления тела (вурфа) образуют систему взаимного пропорционирования и потому оказываются неразделимыми. Надо отметить, что, напримѣр, в живой природе, в биологических телах, в строении тела человека трехчастное деление наблюдается постоянно. Напримѣр: пальцы рук и ног имеют трёхфаланговое строение, руки – трёхчленистое и т.д.”[12] Понимание принципа троичности имело в древнем зодчестве огромное, если не решающее значение, что видно даже из самого слова сТРОИТЬ.
Подводя итог этой главы отметим, что знание пространственных законов, в основе которых лежало понимание пропорциональных матричных зависимостей, позволяло древнерусским мастерам создавать эстетически и архитектурно гармоничные “живые” строения и структуры, которые вследствие пространственно волновой согласованности элементов были в значительно меньшей мѣре подвержены разрушительному влиянию времени. При этом, практически отпадала необходимость в осуществлении точных расчетов в абсолютных величинах, поскольку в голове зодчего всегда находился канон, содержащий принципы гармоничного пропорционирования. Перед историками до сих пор стоит вопрос: куда подевались чертежи возведенных на Руси многочисленных храмов, которые согласно современным представлениям непременно должны были существовать. По нашему мнению ответ прост – таких чертежей нет и никогда не было, вследствие их полнейшей ненадобности в древнерусской системе мѣръ.
В следующей статье будет рассмотрена Древнерусская система измѣрения врѣмени.
Список вспомогательной литературы
- Черняев А.Ф. Золото Древней Руси. — М., 1998.
- Рыбаков Б.А. Русская система мер длины ХI-ХV веков // Сов. эти. 1949. — № 1.
- Кирик Новгородец. Учение имже ведати человеку числа всех лет. Перевод В. П. Зубова и Т. А. Коншиной. Примечания и статья В. П. Зубова.— ИМИ, 1953, № 6
- Пилецкий А.А. Система размеров и их отношений в древнерусской архитектуре. Сборник. Естественнонаучные знания в Древней Руси. — М.: Наука, 1980.
- Коробко В.И., Коробко Г.Н. «Золотая пропорция и человек». – М., 2002.
- Прозоровский Д.И. О старинных русских мерах протяжения // Известия РАО СПб. — 1872.
- Рыбаков Б.А. Архитектурная математика древнерусских зодчих. Из истории культуры Древней Руси. — МГУ, 1984.
- Шмелев И.П. Архитектор фараона. Искусство России. — С.Пб, 1993.
- Матрица древнерусских саженей, имеющих в основе золотую пропорцию или «Всемѣр» Древней Руси. Автор: LSVSX // https://lsvsx.livejournal.com/332294.html
[1] Позднее (1791 г.) специальная комиссия Французского Национального конвента постановила определять метр как “одну сорокамиллионную часть Парижского меридиана (то есть одну десятимиллионную часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа)”. Цит. по Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82.
[2] Приведенные в работе параллели не претендуют на статус абсолютной истины. Возможно наши читатели в комментариях предложат более убедительный ответ на вопрос почему сутки были разделены на 24 части? Однако известно, что согластно традиционному Китайскому времяисчислению сутки делились на 12 частей, в Древней Индии на 30 частей, у индейцев Майя на 22 части. а в революционной Франции конца ХVIII в. на 10 частей.
[3] Черняев А.Ф. Золото Древней Руси. — М., 1998. С.30
[4] Черняев А.Ф. Золото Древней Руси. — М., 1998. С.11
[5] Там же С.14
[6] С точки зрения строго математической терминологии здесь правильнее было бы изпользовать термин “система пропорционировния”. Однако, изпользованием термина в тексте мы хотели подчеркнуть ключевое значение выявления пропорции в процессе измѣрения.
[7] Возможно, что в действительности на практике изпользовался более простой метод: в качестве “местного эталона” бралась любая сажень, примерно соответствующая представлению о среднем значении величины или же “эталонная сажень” сохранившаяся после однажды проведенных измерений.
[8] Матрица древнерусских саженей, имеющих в основе золотую пропорцию или «Всемер» Древней Руси. Автор: LSVSX // https://lsvsx.livejournal.com/332294.html
[9] В работе речь идет лишь о матрицах со взаимозависимыми элементами.
[10] Приведенное в тексте определение наше.
[11] Данная зависимость описывается числовым значением или математической функцией.
[12] Коробко В.И., Коробко Г.Н. «Золотая пропорция и человек». – М., 2002.